What's the Problem?

Above is an equilateral triange and its circumcircle. Let's say the length of a side of the triangle is 'a', and the circumcircle is called 'O'. In this case, what would the percentage of a random chord in circle O's length exceeding 'a'?
Expected Answers
1) 1/3

2) 1/4
Using Python
Script 1 _ Random X Coordinate Point
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
import random
import math
import turtle as t
# variables
xa=0
ya=0
xb=0
yb=0
d=0
y=0
big=[]
i=0
j=0
r1=200
r2=1
f=[]
c='none'
tf=0
final=0
#axis
t.speed(0)
t.penup()
t.goto(-400,-300)
t.pendown()
t.goto(400,-300)
t.penup()
t.goto(-400,-300)
t.pendown()
t.goto(-400,300)
# program
t.hideturtle()
t.penup()
t.goto(200,100)
t.pendown()
t.circle(100)
while j<r2:
while i<r1:
xa=random.random()
y=[math.sqrt((1/4)-(xa-1/2)**2),-(math.sqrt((1/4)-(xa-1/2)**2))]
ya=random.choice(y)
xb=random.random()
y=[math.sqrt((1/4)-(xb-1/2)**2),-(math.sqrt((1/4)-(xb-1/2)**2))]
yb=random.choice(y)
d=math.sqrt((xa-xb)**2+(ya-yb)**2)
if d>=math.sqrt(3/4):
big=big+[d]
c='red'
tf=1
else:
c='black'
tf=0
i=i+1
#circle graphics
t.penup()
t.goto(200*(xa-1/2)+200,200*(ya)+200)
t.pendown()
t.color(c)
t.goto(200*(xb-1/2)+200,200*(yb)+200)
#graph
t.penup()
t.goto((800/r1)*(i-1)-400,600*((len(big)-tf)/i)-300)
t.pendown()
t.goto((800/r1)*(i)-400,600*(len(big)/(i+1))-300)
f=f+[(len(big)/r1)*100]
j=j+1
final=float(sum(f)/len(f))
t.write(final,False,"right",("",15))
print(final)
|
cs |
<Result>

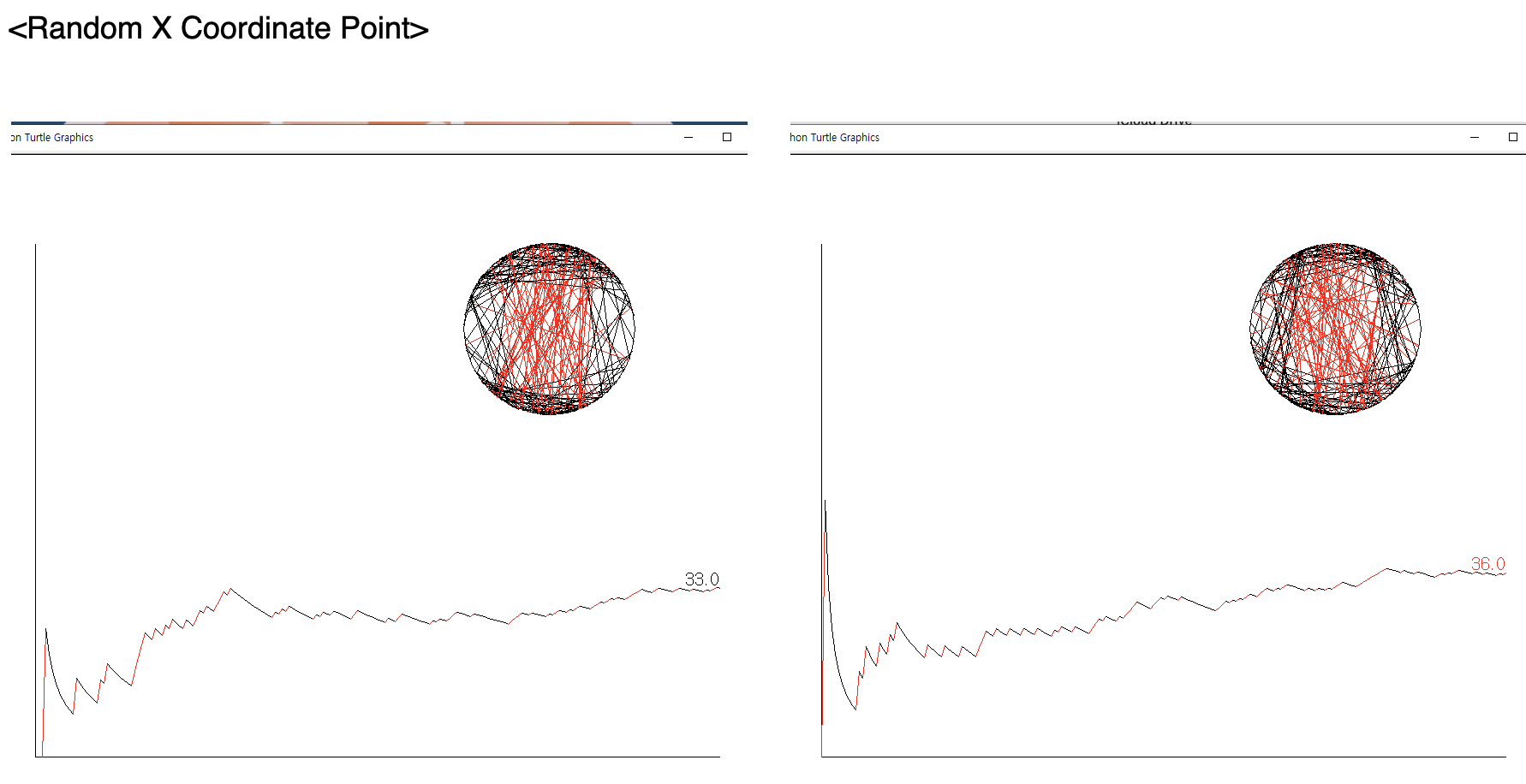
Script 2 _ Random Angle Point
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
|
import random
import math
import turtle as t
#variables
radian=0
xa=0
ya=0
xb=0
yb=0
big=[]
c='none'
r1=200
r2=1
tf=0
i=0
j=0
final=[]
result=0
#grid
t.speed(0)
t.penup()
t.goto(-400,-300)
t.pendown()
t.goto(400,-300)
t.penup()
t.goto(-400,-300)
t.pendown()
t.goto(-400,300)
#program
t.hideturtle()
t.penup()
t.goto(200,100)
t.pendown()
t.circle(100)
while j<r2:
while i<r1:
radian=2*(random.random())*(math.pi)
xa=1*math.cos(radian)
ya=1*math.sin(radian)
radian=2*(random.random())*(math.pi)
xb=1*math.cos(radian)
yb=1*math.sin(radian)
d=math.sqrt((xa-xb)**2+(ya-yb)**2)
if d>=math.sqrt(3):
big=big+[d]
c='red'
tf=1
else:
c='black'
tf=0
i=i+1
#circle graphic
t.penup()
t.goto(100*xa+200,100*ya+200)
t.pendown()
t.color(c)
t.goto(100*xb+200,100*yb+200)
#graph
t.penup()
t.goto((800/r1)*(i-1)-400,600*((len(big)-tf)/i)-300)
t.pendown()
t.goto((800/r1)*(i)-400,600*(len(big)/(i+1))-300)
final=final+[(len(big)/r1)*100]
j=j+1
result=float(sum(final)/len(final))
t.write(result,False,"right",("",15))
print(result)
|
cs |
<Result>

'Ideas & Experiments' 카테고리의 다른 글
| Light and Collision(빛의 충돌현상에 대하여) (0) | 2021.03.06 |
|---|---|
| Ideas on the Universe & the Big Bang (0) | 2021.03.01 |
| Expansion of Kepler's 3rd Law of Planetary Motion (0) | 2021.03.01 |
| Integral of linear polynomials raised to the nth power (0) | 2021.03.01 |
| A Theory on the Grandfather Paradox (0) | 2021.02.01 |

