A week ago, while caculating maxium distance of projectile with the effects of drag, I faced a problem. To find the velocity function of the projectile related to time, I had to solve an equation involving the inegral of the square of the velocity function. Since the only thing I knew about integration was multiplying ax^n with x and dividing it by n+1, I had no idea how to move on. So, hoping that I would be able to find an equation for ∫f(x)^2 dx, I started calculating the indefinite intergrals of (2x+1)^2, (6x+2)^2, (5x-1)^2, and many more. What I found out is that ∫(ax+b)^2 dx = ((ax+b)^3)/3a. With this hypothesis in mind, l did the calculations for general cases.
∫(ax+b)^2 dx = ?
proof)
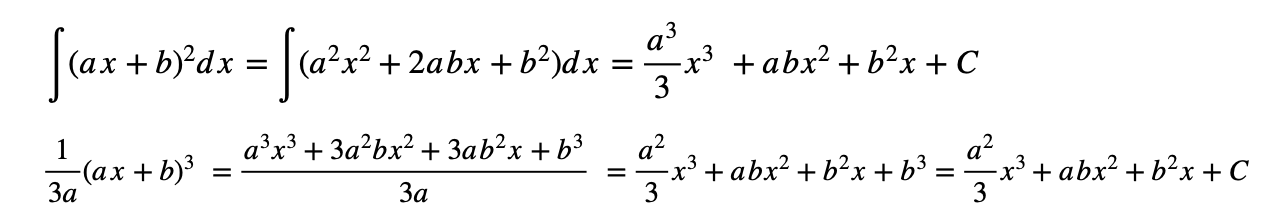
∫(ax+b)^n dx = ?
Next, I derived the general formula by expressing the nth-powered polynomial with binomials, and then integrating it.
This is how I did it:
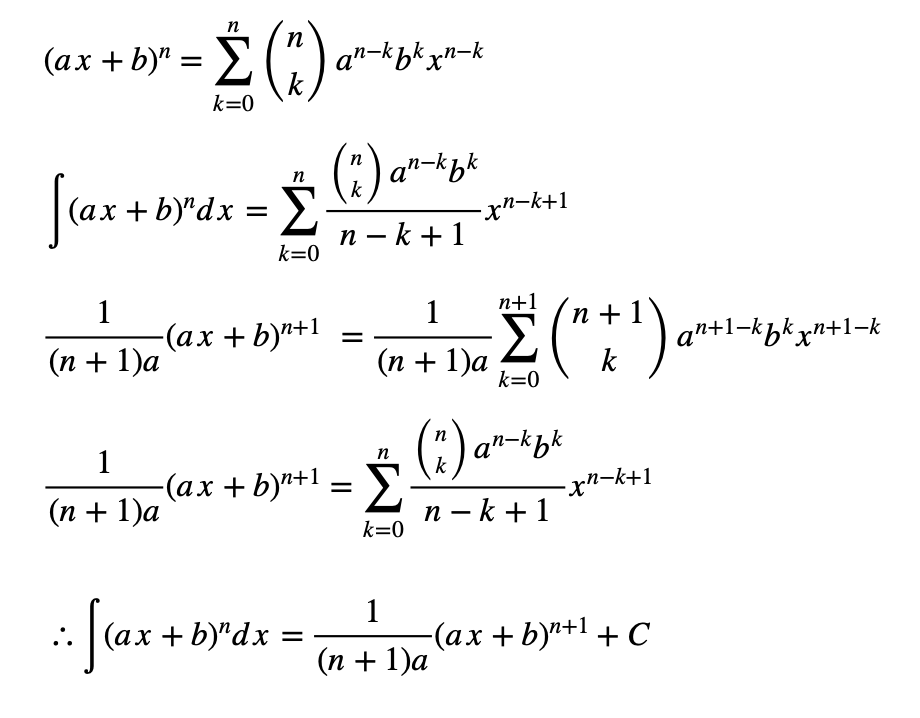
It was fun discovering a pattern and proving it mathematically. My plans in the near future are to derive another equation on myself ; not just about linear polynomials, but the integral of f(x)^n.
+) I later found out that the method integrating linear polynomials already exists(as expected). Even so, I think this was a good chance to test my mathematical skill.
'Ideas & Experiments' 카테고리의 다른 글
| Ideas on the Universe & the Big Bang (0) | 2021.03.01 |
|---|---|
| Expansion of Kepler's 3rd Law of Planetary Motion (0) | 2021.03.01 |
| A Theory on the Grandfather Paradox (0) | 2021.02.01 |
| Relation between Time and Velocity in Special Relativity (0) | 2021.01.30 |
| Pattern of palindromes(팔린드롬의 규칙) (0) | 2020.03.07 |